Implementing Bubble Sort in Javascript - with an interactive webapp

How the algorithm works

Bubble sort runs on two iteration levels.

1. The outer iteration is executed once per array item

2. The inner iteration is performed until the current item is to the left of an item that has a higher value or at the end of the array.

• The inner iteration simply compares the current item to the item to the left
• If the current item's value is higher than it's neighbors value, both items are swapped
• If not, nothing happens and the inner iteration moves on.
• When all items are sorted, the algorithm is done.

How I tackled this algorithm in a fun way

I found all explanations on the internet (including the one you just read) dull. I figured it would be way more fun to have something to visualize what's going on under the hood.

If you're after the code, scroll down to the implementation details

So I created an application that would allow me to walk through the algorithm step by step. You can find it here, in this code sandbox.

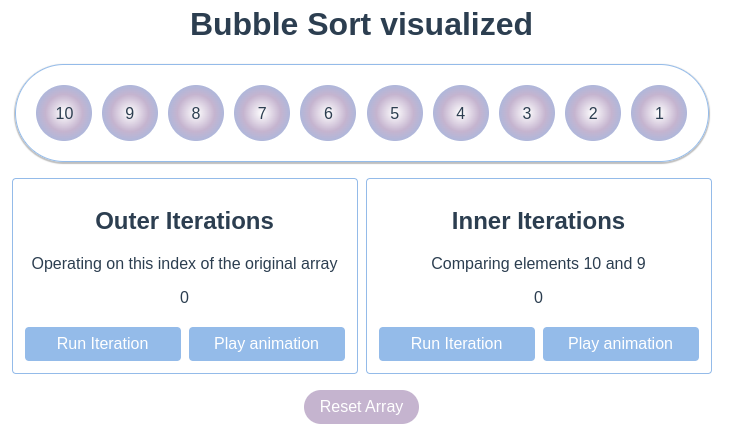
• The two windows you can see control the algorithm's inner and outer iterations. When clicking on 'Run Iteration', the app will perform a single algorithm step.
• The initial array is simply an unordered list of numbers starting with 10, ending with 1.

The inner iteration

Let's start slowly by iterating only a single time over our array.

The inner iteration - Step 1

• We start with the first element. It has a value of 10.
• Bubble sort will now compare this value and the next value in the array
• Since 10 > 9, it will switch out these two elements

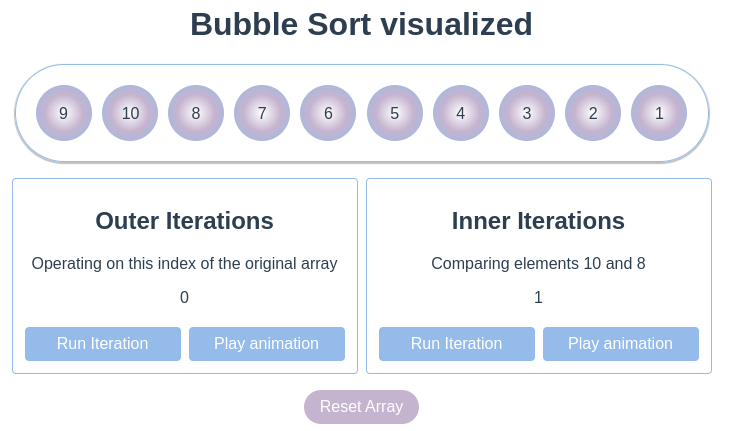
The inner iteration - Step 2

• We are still comparing 10 with its next element.
• The value of the next element is 8
• Since 10 > 8, it will switch out these two elements

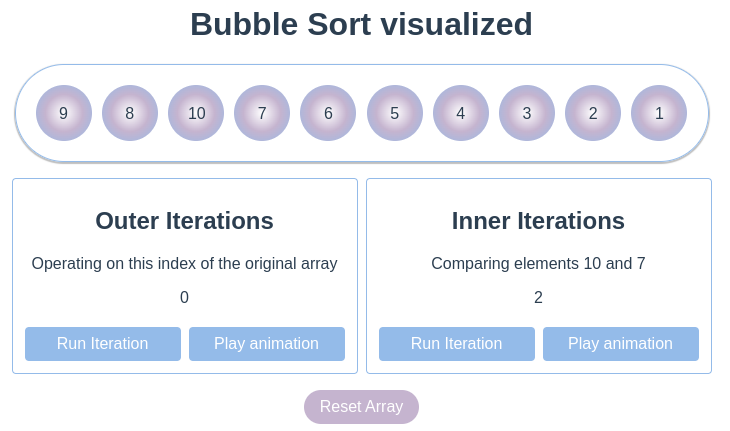
The inner iteration - Step n

This procedure will continue until the end of the array is reached. The number 10 is now at its correct position and all other elements were moved one place to the left.

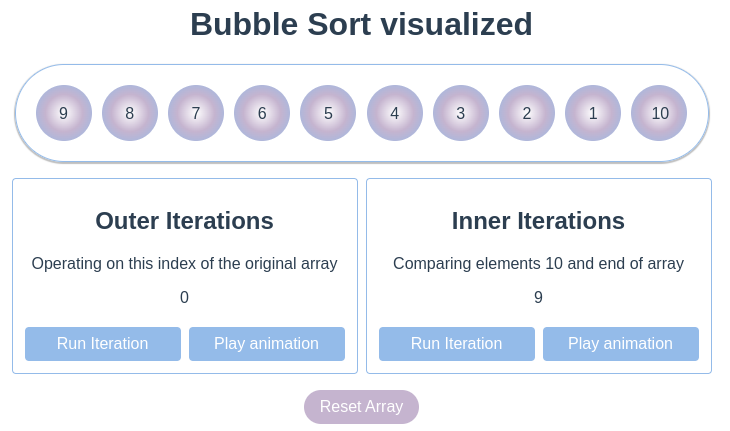
Bubble sort operates by literally 'bubbling' the biggest number it can find to the end of the array.

This concludes the inner iteration for the number 10. When clicking on 'Run Iteration' in the 'Inner Iterations' card again, the 'Outer Iterations' counter will increase and we can move on.

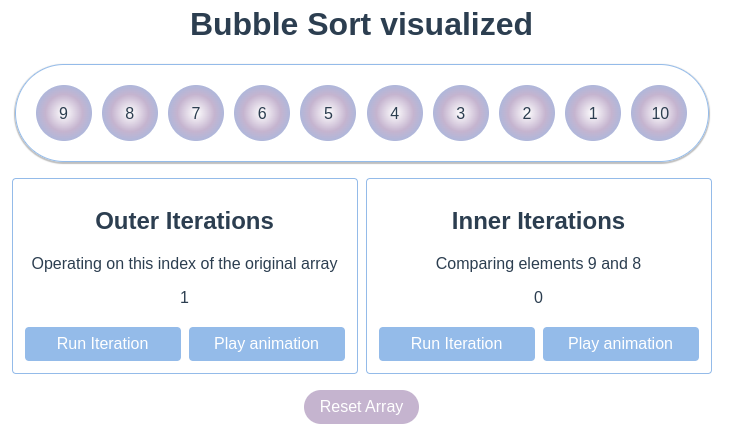
The outer iteration

We just went through a whole inner iteration step-by-step. The outer iteration simply applies this logic to every element till the end of the array is reached.

The outer iteration - Step 1

Assuming we continue where we left in 'The inner Iteration', the result of the first step would look like this:

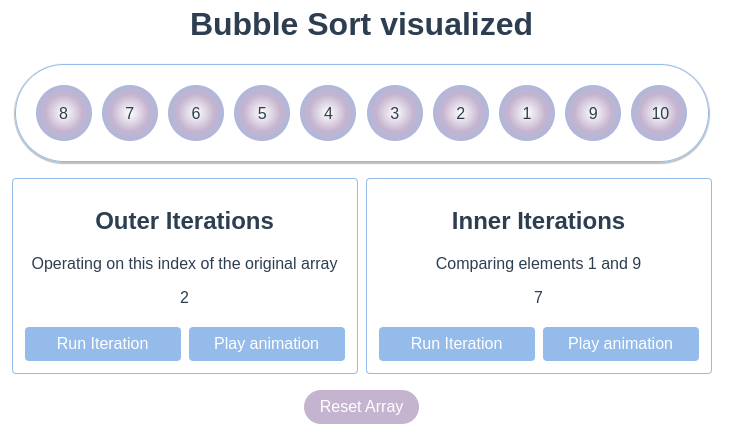
This time, the number 9 bubbled to the end of the array & the final comparison was to compare the elements 1 and 9.

The outer iteration - Step 2

Let's do this again and bubble 8 up:

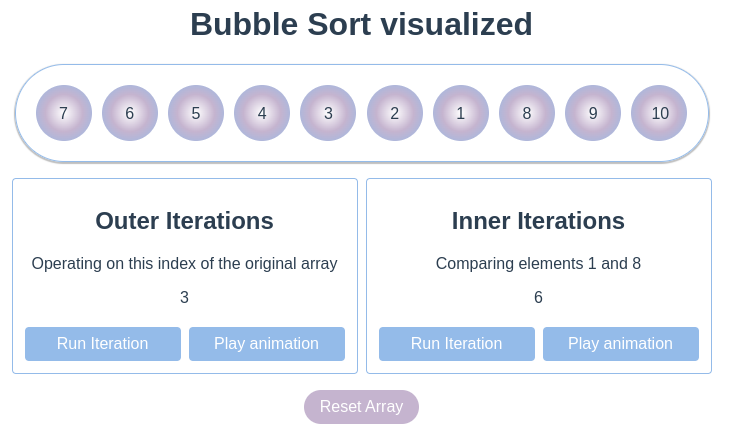
The outer iteration - Step n

After bubbling all the numbers up, eventually the correct order will look like this:

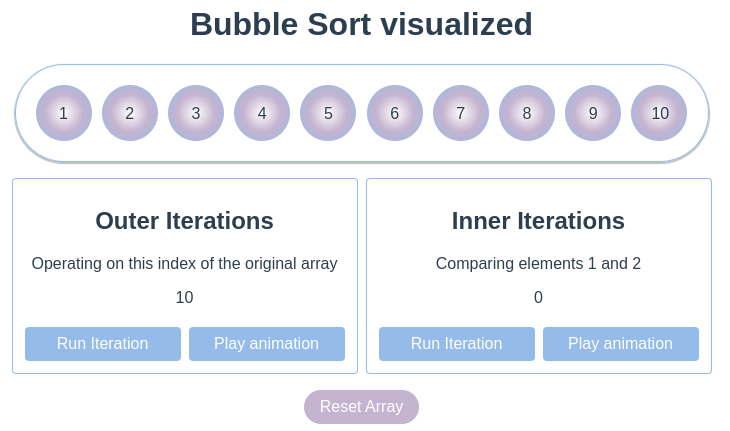
Since all elements are now in the correct order, the algorith has done its job. And our list of numbers is sorted.

Implementation details - the code

The code to perform all these single steps looks like this. In the code sandbox, you might find the one or another tweak to display the indicator numbers correctly. At its core, the check is always the same though.

const numbers = [4, 3, 2, 1];

function bubbleSort(array) {
	const localArray = [...array];
	const itemCount = localArray.length;

	// For each item in the array
	for (let currentIteration = 0; currentIteration < itemCount; currentIteration++) {

		// Move one step to the right until last unsorted item is reached
    const sortedItemCount = itemCount - currentIteration - 1;
		for (let bubbleStep = 0; bubbleStep < sortedItemCount; bubbleStep++) {

      // Is the currently indexed item greater than its next element?
      // If yes, switch the two elements
      // If not, do nothing and continue to the next element
      if(localArray[bubbleStep] > localArray[bubbleStep + 1]) {
        const temp = localArray[bubbleStep];
        localArray[bubbleStep] = localArray[bubbleStep + 1];
        localArray[bubbleStep + 1] = temp
      }
    }
  }
  return localArray
}

const sortedNumbers = bubbleSort(numbers)
console.log(sortedNumbers) // [1, 2, 3, 4]