Queues help you to process data using the FIFO (first in, first out) principle. They're specifically great for managing events or asynchronous tasks. Unless other languages, like Java or Python, Typescript does not have its own native Queue class. So let's build some ourselves
Table of contents
I briefly touched on the Queue topic of managing window scroll events in a previous article. Using a native array to handle event tasks works for small examples. When it comes to performance and scalability, it's not a good choice, because
shiftcauses the array to re-index every item, which is computationally expensive- resizing the array can cause memory fragmentation and garbage collection overhead
- arrays are optimized for indexing tasks (~= accessing items), not frequent I/O
The Queue implementations in this article still use arrays under the hood, but handle their data more efficiently. Let's dive in.
A default array Queue
Let's look at a simple example. We'll build a Queue structure with some default operations and an array and add the optimizations later.
Every Queue has a minimum of two operations:
enqueueto add new items to the backdequeueto retrieve the item in the front and effectively remove it from the Queue
We will also add some commonly used methods:
lengthto print the Queue's lengthemptyto see if the Queue contains any itemspeekto display the item in the front without removing it
The following image should give you an idea of what it will look like:
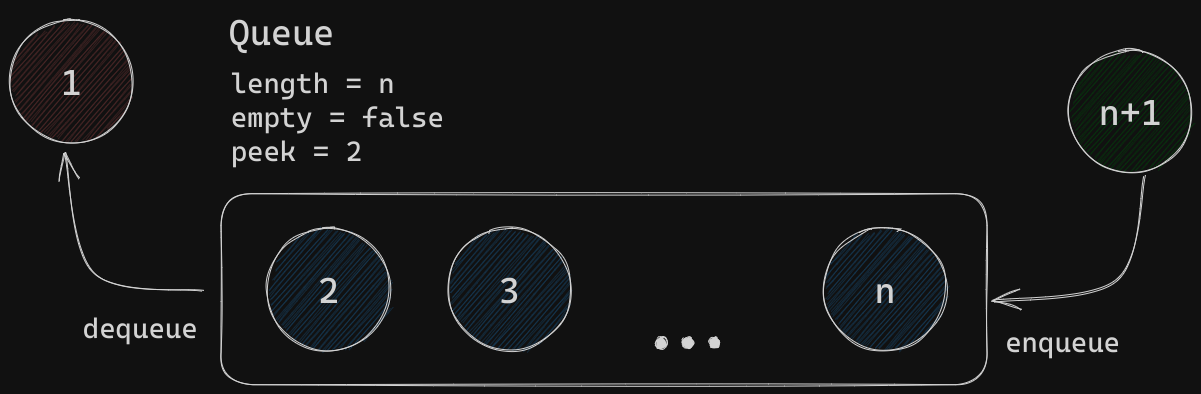
The code for this entity uses Typescript class syntax and a generic to ensure data consistency.
class SimpleArrayQueue<T> {
private readonly store: T[] = [];
public get length(): number {
return this.store.length;
}
public get empty(): boolean {
return this.store.length === 0;
}
public peek(): T | undefined {
return this.store[0];
}
public enqueue(item: T) {
this.store.push(item);
}
public dequeue(): T | undefined {
return this.store.shift();
}
}
You can try this implementation out in a REPL or Quokka if you're using VSCode.
const queue = new ArrayQueue<number>();
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
// Check the first item in the queue
const peek = queue.peek(); // 1
console.log(peek);
// Remove the first item from the queue
console.log(queue.dequeue()); // 1
// Check the first item again
const peek2 = queue.peek(); // 2
console.log(peek2);
This should give you an idea of how a Queue basically works. However, using a simple array wrapped in a class doesn't provide much value over shifting and pushing. Let's look at the optimisations next.
The Dynamic Array-based Queue
There are many approaches to designing a Queue on the Internet. All of them use similar APIs to the basic one we just built but have their own ways of handling memory. So I decided to reinvent the wheel. I can't just copy/paste stuff all the time, can I?
The Queue I wanted was to be
- above all: easy to understand and implement
- efficient in terms of performance and memory usage
- scalable if necessary
This implementation is inspired by the Circular Buffer Queue, which we'll look at later in the article. Its approach to handling dequeued elements is different, but easier to understand and use.
Instead of handling a lot of logic internally, the Dynamic-Array-based Queue lets the developer decide its boundaries.
- The constructor accepts an
indexingThresholdand amaxLength indexingThresholddetermines when the Queue is re-indexed (=when all dequeued elements are recycled), but has a high computational cost as the array growsmaxLengthensures uncontrollable growth of the array, but requires careful handling by the developer as not to accidentally drop elements
Params indexFront and indexBack are borrowed from the Circular Buffer Queue to determine where to enqueue and dequeue elements.
The following describes the approach in detail using sketches and some descriptions. If you're after the code, feel free to skip the following section and jump straight to the code.
How it works
I find this approach hard to describe using text, so I sketched it. These sketches assume:
- a
maxLengthof 5 - an
indexingThresholdof 2 - an initial size of 0
Enqueue elements
Let's add 5 elements, for example, the numbers 1 - 5
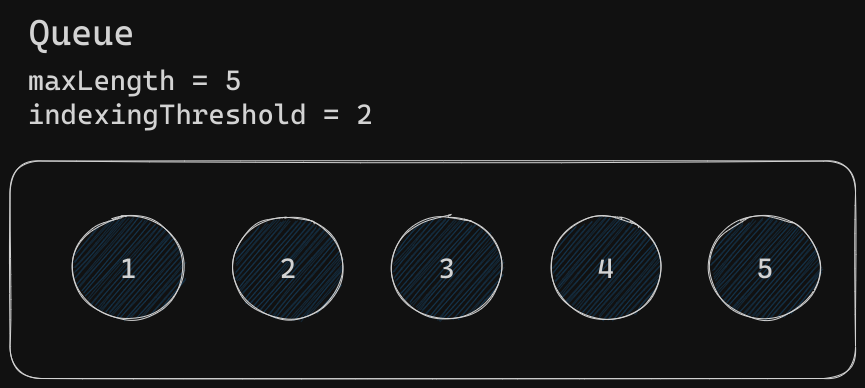
If we try to add more elements, we'll hit a limit here. The Queue does not accept any further items. Which is fine and what we would expect.
Dequeue 2 elements
Assume the first two elements are dequeued. In their place, an undefined value would take place while the indexFront variable is incremented
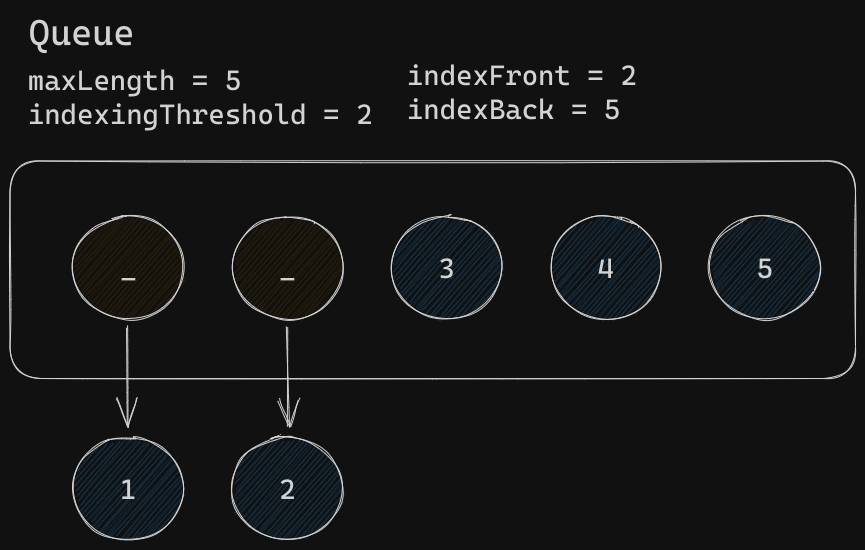
Enqueue 1 element
Here's where it gets interesting. Once a new element is added to the Queue while it exceeds the indexingThreshold, it triggers a method called updateIndexes before the item is added. This method moves all non-undefined values to the start of the Queue and updates the indexFront and indexBack parameters.
Let's walk through this step by step.
First, enqueue is called
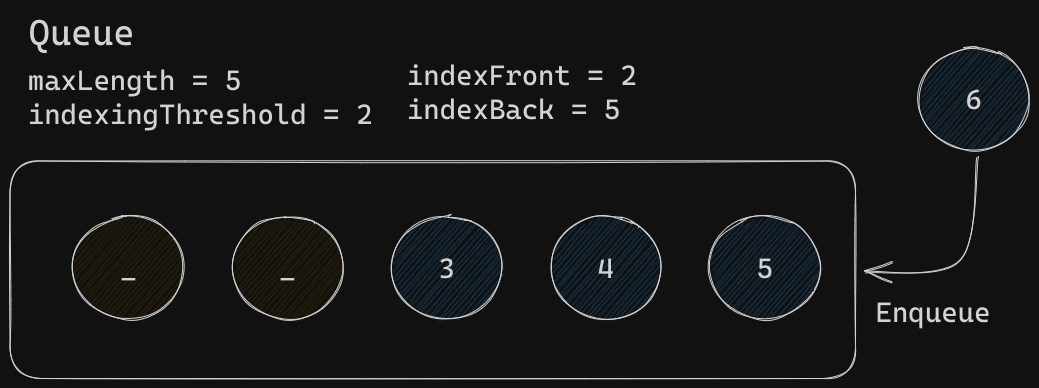
Since indexFront is equal to indexingThreshold, we will move all undefined elements to the end of the Queue first. This also sets the front- and back-index to their appropriate values.
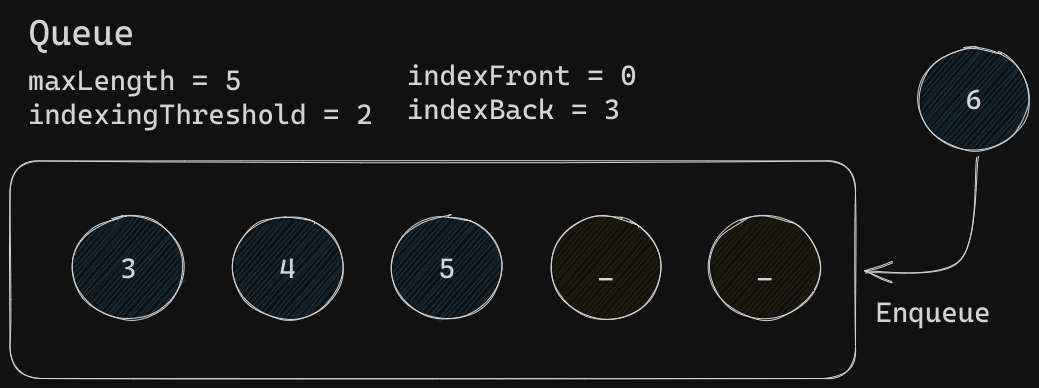
Finally, the new element will be added to the Queue. Notice how the size of the Queue has not changed and no possibly inefficient re-indexing took place
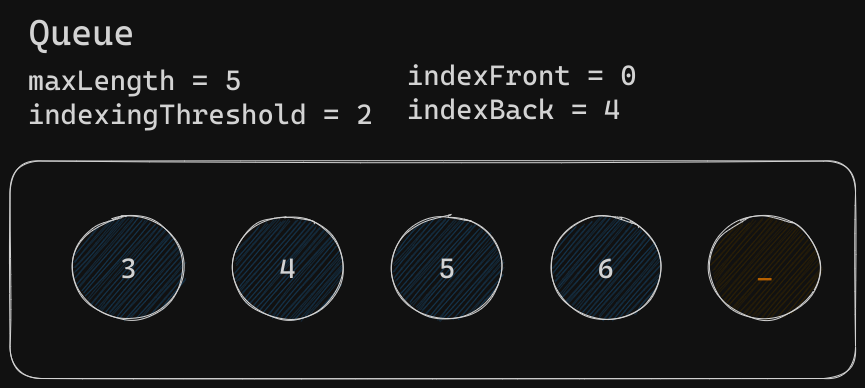
Show me the code
Here's the full implementation that follows this exact specification.
class Queue<T> {
private store: T[] = [];
private indexFront: number = 0;
private indexBack: number = 0;
private cleanupThreshold: number;
private maxLength: number;
constructor({
items,
cleanupThreshold,
maxLength,
}: { items?: T[]; cleanupThreshold?: number; maxLength?: number } = {}) {
this.cleanupThreshold = cleanupThreshold ?? 10_000;
this.maxLength = maxLength ?? Number.MAX_SAFE_INTEGER - 1;
this.init(items);
}
private init(items?: T[]) {
// Indexing threshold cannot be negative
if (this.cleanupThreshold <= 0) {
throw new Error("Indexing threshold cannot be zero or negative");
}
// Max length cannot be negative
if (this.maxLength && this.maxLength <= 0) {
throw new Error("Max length cannot be zero or negative");
}
// Initial items size cannot exceed max length of Queue
if (items && this.maxLength && items.length > this.maxLength) {
throw new Error("Initial items length cannot be greater than max length");
}
// Initialize the queue with the provided items
if (items && items.length > 0) {
this.indexBack = items.length;
this.store = items.slice();
}
}
get length() {
return this.indexBack - this.indexFront;
}
get empty() {
return this.length === 0;
}
get full() {
return this.length >= this.maxLength;
}
public enqueue = (item: T) => {
if (this.full) {
console.warn("Queue is full, item will not be added");
return;
}
if (this.indexFront >= this.cleanupThreshold) {
this.updateIndexes();
}
this.store[this.indexBack] = item;
this.indexBack++;
};
public dequeue = () => {
if (this.empty) {
console.warn("Cannot dequeue, queue is empty");
return undefined;
}
const item = this.store[this.indexFront];
this.store[this.indexFront] = undefined as unknown as T; // Clear the slot
this.indexFront++;
return item;
};
public peek = () => {
if (this.empty) {
console.warn("Cannot peek, queue is empty");
return undefined;
}
return this.store[this.indexFront];
};
private updateIndexes() {
// Shift all non-undefined elements to the start of the array
let writeIndex = 0;
for (let i = this.indexFront; i < this.indexBack; i++) {
const item = this.store[i];
if (item !== undefined) {
this.store[writeIndex] = item;
if (i !== writeIndex) {
this.store[i] = undefined as unknown as T;
}
writeIndex++;
}
}
this.indexBack = writeIndex;
this.indexFront = 0;
}
}
A Circular Buffer Queue
While the above method works well for small and medium Queue sizes, it is generally outperformed by a Circular Buffer Queue. Since this article focuses on the former, I'll make it quick and simply provide you with the code and get straight to the benchmark
I created this function together with ChatGPT, I'm sure you'll understand I'll save you the time of walking you through the process
class CircularBufferQueue<T> {
private store: T[];
private frontIndex: number; // Points to the first element
private backIndex: number; // Points to the position where the next element will be added
private capacity: number;
constructor({
initialCapacity,
items,
}: { initialCapacity?: number; items?: T[] } = {}) {
this.store = new Array(initialCapacity || 10);
this.frontIndex = 0;
this.backIndex = 0;
this.capacity = initialCapacity || 10;
if (items && items.length > this.capacity) {
this.resize(items.length);
}
if (items) {
for (const item of items) {
this.enqueue(item);
}
}
}
get length(): number {
return this.backIndex - this.frontIndex;
}
get empty(): boolean {
return this.length === 0;
}
enqueue(item: T): void {
if (this.length === this.capacity) {
this.resize(this.capacity * 2); // Double the capacity when full
}
this.store[this.backIndex % this.capacity] = item;
this.backIndex++;
}
dequeue(): T | undefined {
if (this.empty) {
console.warn("Cannot dequeue, the queue is empty");
return undefined;
}
const item = this.store[this.frontIndex % this.capacity];
this.store[this.frontIndex % this.capacity] = undefined as any; // Clear the slot
this.frontIndex++;
if (this.length > 0 && this.length <= this.capacity / 4) {
this.resize(this.capacity / 2);
}
return item;
}
peek(): T | undefined {
if (this.empty) {
return undefined;
}
return this.store[this.frontIndex % this.capacity];
}
private resize(newCapacity: number): void {
const newStore = new Array(newCapacity);
let writeIndex = 0;
// Copy valid elements to the new array
for (let i = this.frontIndex; i < this.backIndex; i++) {
newStore[writeIndex] = this.store[i % this.capacity];
writeIndex++;
}
this.store = newStore;
this.capacity = newCapacity;
this.frontIndex = 0;
this.backIndex = writeIndex;
}
}
Benchmarking both implementations
I was curious whether the circular buffer method generally outperforms my own approach, so I did a few test runs on my laptop with the following specifications. It's not a fully-fledged benchmark from the textbooks but should give us some performance insights.
Input specifications
I have tried four scenarios.
- Process the numbers (integers) from 1 to 500.000.000
- Process a small object 500.000.000 times
- Process a complex object 500.000.000 times
I'm running all of these tests in the Deno runtime using deno run
Results for numbers
The three runs for the Circular Buffer Queue were
- 2.778 seconds
- 2.718 seconds
- 2.758 seconds
while three runs for the Dynamic Array-Based Queue were
- 2.560 seconds
- 2.612 seconds
- 2.513 seconds
which I was able to improve by setting maxLength to 25 and cleanupThreshold to 5.
- 2.017 seconds
- 2.067 seconds
- 2.039 seconds
To be fair, the initial results might be caused by a design flaw (I set the default maxLength to Number.MAX_SAFE_INTEGER and cleanupThreshold to 10.000).
Results for small objects
The object in question is
const o = {
id: i, // dynamically calculated from 1 - 500.000.000
name: "John Doe",
age: 30,
address: "123 Main St",
city: "Anytown",
state: "CA",
zip: "12345",
country: "USA"
}
The three runs for the Circular Buffer Queue were:
- 6.840 seconds
- 6.784 seconds
- 6.866 seconds
The three runs for the Dynamic Array-Based Queue (I kept the maxLength and cleanupThreshold without running into problems) were:
- 6.401 seconds
- 6.308 seconds
- 6.107 seconds
Results for more complex objects
The object in question is 220 lines long - you can find it in this Gist. To save time, I've reduced the sample size to 5.000.000 complex objects instead of 50.000.000 for these runs.
Results for Circular Buffer Queue were:
- 43.208
- 43.136
- 43.645
The results for the Dynamic Array-Based Queue were
- 43.245
- 43.747
- 43.457
On average, the Circular Buffer Queue behaved a bit better.
Wrap up
The Dynamic Array-Based Queue behaved better than I expected. Be aware that I only tested throughput for these two elements. Under real circumstances and different hardware, it is possible (and likely) for both implementations to behave very differently.


